La moyenne mobile de Kaufman (KAMA) a été introduit par Perry J. Kaufman en 1995 dans son livre : Smarter Trading. La moyenne mobile de Kaufman est une moyenne mobile adaptative qui permet d’ajuster sa vitesse par rapport au niveau d’agitation des cours actuels.
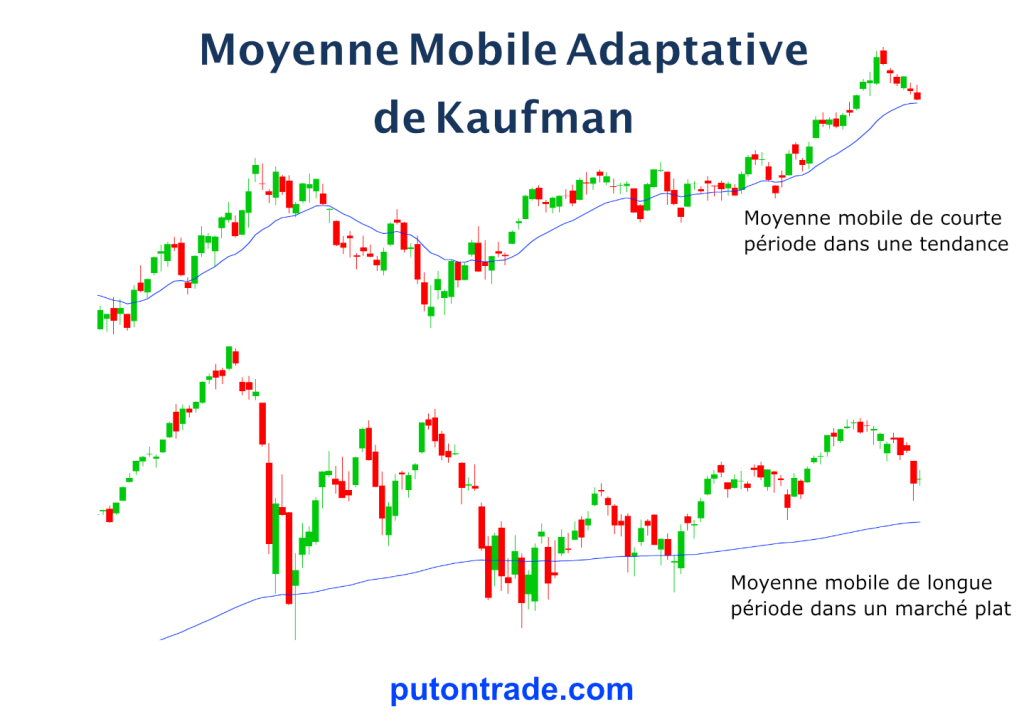
Figure-1 : modèle graphique de la moyenne mobile adaptative.
La figure-1 montre un exemple de la moyenne mobile adaptative, lorsque le marché est en tendance la période de la moyenne mobile est courte et lorsque le marché est plat la période de la moyenne mobile est longue.
La méthode de calcul
La moyenne mobile de Kaufman utilise la formule de calcul de la moyenne mobile exponentielle comme la majorité des moyennes mobiles adaptatives :
Moyenne Mobile de Kaufman (KAMA) = Moyenne Mobile de Kaufman précédente (KAMA – 1) + facteur d’ajustement x (cours de clôture – Moyenne Mobile de Kaufman précédente (KAMA – 1))
Facteur d’ajustement = [ratio d’efficacité x (multiplicateur de la limite courte – multiplicateur de la limite longue) + multiplicateur de la limite longue] à puissance 2.
Ratio d’efficacité = valeur absolue (cours de clôture – cours de clôture (n) jours) / somme de (n) jours (valeur absolue (cours de clôture – cours de clôture précédent)).
Cependant, le calcul du facteur d’ajustement dépend de trois variables : la période pour calculer le ratio d’efficacité (ER : Efficiency Ratio) qui mesure le niveau d’agitation des cours sur une période, la limite longue et la limite courte.
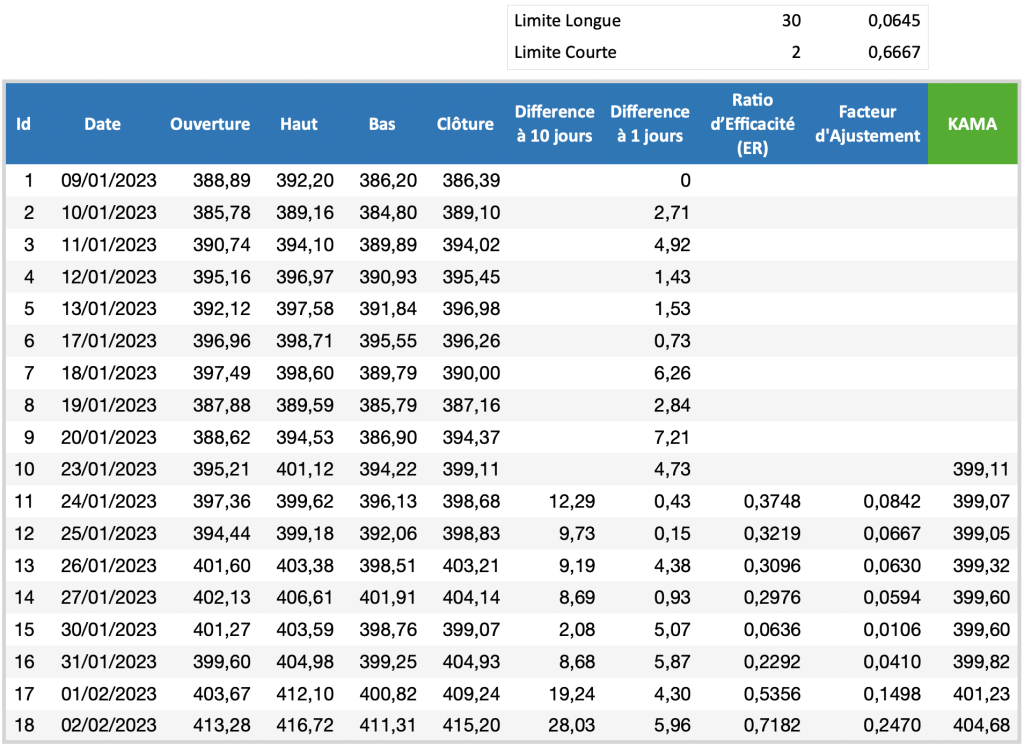
Le tableau suivant présente un exemple de calcul de la moyenne mobile de Kaufman sur les cours de clôtures journaliers de SPDR S&P 500 ETF avec les valeurs par défaut préconisées par Kaufman : la période de 10 pour le calcul ratio d’efficacité (ER), 30 pour la limite longue et 2 pour la limite courte.
- La première valeur de la KAMA au 23/01/2023 est égale au cours de clôture 399,11.
- Calculer le multiplicateur de la limite longue = 2 / (1 + 30) = 0,0645 et le multiplicateur de la limite courte = 2 / (1 + 2) = 0,6667.
- Calculer en valeur absolue la différence des cours de clôture à 10 jours. Par exemple au 24/01/2023 la différence à 10 jour = 398,68 (cours de clôture au 24/01/2023) – 386,39 (cours de clôture au 09/01/2023) = 12,29. Si le résultat est négatif, pendre la valeur absolue pour qu’il soit toujours positif.
- Calculer en valeur absolue la différence des cours de clôture à 1 jour. Par exemple au 10/01/2023 la différence à 1 jour = 389,10 (cours de clôture au 10/01/2023) – 386,39 (cours de clôture au 09/01/2023) = 2,71. Si le résultat est négatif, pendre la valeur absolue pour qu’il soit toujours positif.
- Calculer le ratio d’efficacité qui est égal à la différence à 10 jours divisée par la somme des 10 dernières différences à 1 jour. Par exemple au 24/01/2023 la différence à 10 jours est égal à 12,29 et la somme des 10 dernières différences à 1 jour est égale = 2,71 + 4,92 + 1,43 + 1,53 + 0,73 + 6,26 + 2,84 + 7,21 + 4,73 + 0,43 = 32,79. Donc le ER = 12,29 / 32,79 = 0,3748.
- Finalement le facteur d’ajustement au 24/01/2023 = [0,3748 x (0,6667 – 0,0645) + 0,0645] puissance 2 = 0,2902 ^ 2 = 0,0842
- La KAMA au 24/01/2023 est égale à 399,11 + 0,0842 x (398,68 – 399,11) = 399,07.
- Ainsi de suite
Interprétation
La moyenne mobile de Kaufman est utilisée dans les systèmes de tendance pour identifier le début de la tendance. En effet, un signal d’achat est généré lorsque la pente de la moyenne mobile de Kaufman change de direction, elle passe de baissier à haussier. Ainsi, un signal de vente est généré lorsque la pente de la moyenne mobile Kaufman passe de haussier à baissier.
Exemples
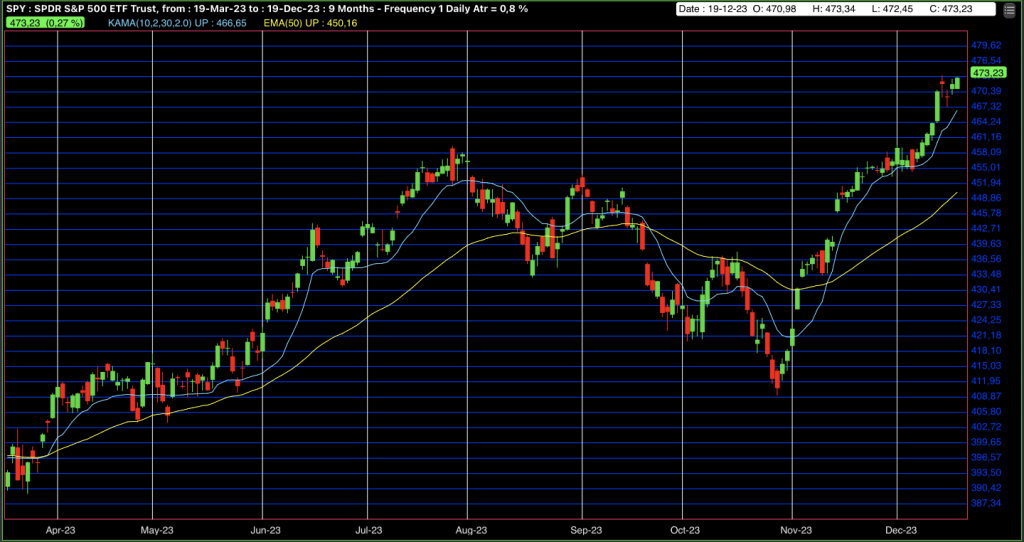
La figure-2 montre les cours journaliers de SPDR S&P 500 ETF avec en jaune la moyenne mobile exponentielle de 50 jours et en bleu la moyenne mobile de Kaufman de 10 jours pour le calcul du ratio d’efficacité, limite courte de 2 et limite longue de 30.
Il est intéressant d’observer comment la période de la moyenne mobile de Kaufman change par rapport à l’agitation des cours. Comme par exemple entre mi-Avril 2023 et mi-Mai 2023 elle est devenue longue lorsque les cours sont passés en trading range. Puis à partir de Juin 2023 la période est devenue courte pour accompagner la hausse des cours. En revanche, la période de la moyenne mobile exponentielle est toujours constante.