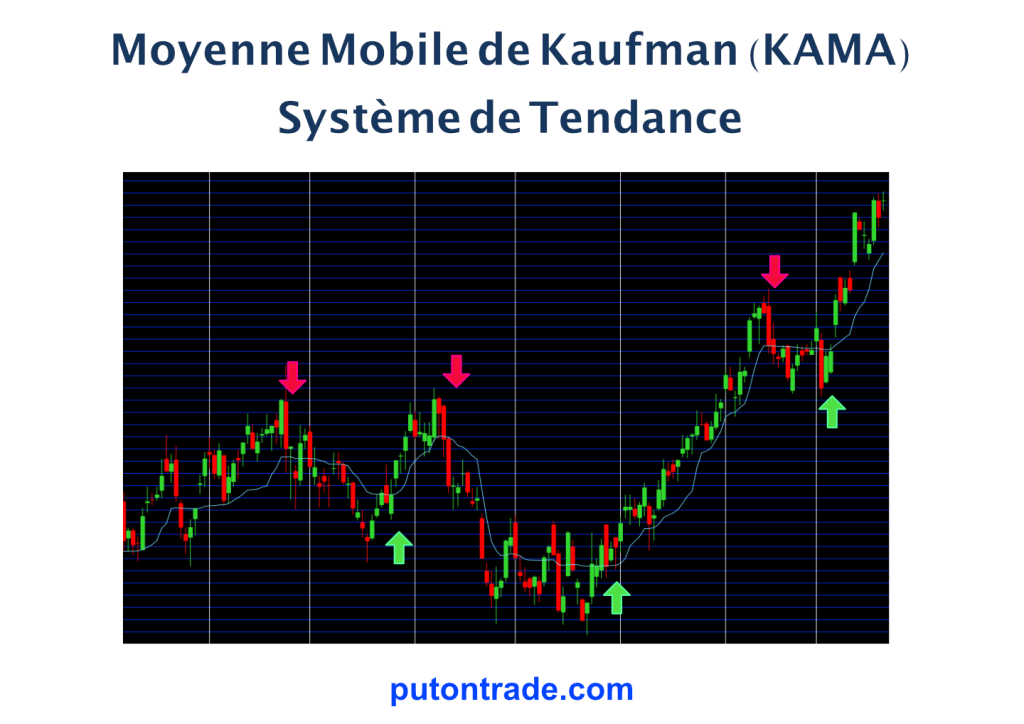
La moyenne mobile de Kaufman (KAMA) est une moyenne mobile adaptative qui permet d’ajuster sa vitesse par rapport au niveau d’agitation des cours actuels. Elle est utilisée dans les systèmes de tendance pour identifier le début de la tendance par l’orientation de la pente de la moyenne mobile.
Le précédent article Moyenne Mobile de Kaufman – Partie 1 présente l’environnement technique global ainsi qu’un exemple graphique de la moyenne mobile de Kaufman. La partie 2 exposera le calcul du Facteur d’ajustement et les performances de la moyenne mobile de Kaufman dans un système de tendance.
Limite longue et la limite courte
Pour rappel la formule de calcul de la moyenne mobile Kaufaman est la suivante :
Moyenne Mobile de Kaufman (KAMA) = Moyenne Mobile de Kaufman précédente (KAMA – 1) + facteur d’ajustement x (Prix de clôture – Moyenne Mobile de Kaufman précédente (KAMA – 1))
Facteur d’ajustement = [ratio d’efficacité x (multiplicateur de la limite courte – multiplicateur de la limite longue) + multiplicateur de la limite longue] à puissance 2.
Ratio d’efficacité = valeur absolue (cours de clôture – cours de clôture (n) jours) / somme de (n) jours (valeur absolue (cours de clôture – cours de clôture précédent)).
Kaufman préconise d’utiliser une période entre 8 et 14 jours pour le calcul du ratio d’efficacité, ainsi qu’une limite longue qui ne dépasse pas 30 jours et une limite courte supérieure à 2 jours.
Le ratio d’efficacité (ER) mesure le dynamise des cours sur une période, sa valeur varie entre 0 et 1. En effet, lorsque le niveau d’agitation des cours est élevé, le ratio d’efficacité (ER) penche vers zéro ce qui augmente la période de la moyenne mobile, à l’inverse, lorsque le niveau d’agitation des cours est faible, le ratio d’efficacité (ER) se rapproche de 1 pour réduire la période de la moyenne mobile.
La limite longue et la limite courte constituent la valeur maximale et la valeur minimale que la période de la moyenne mobile peut avoir. En réalité, il faut appliquer la formule du facteur d’ajustement pour connaitre la vraie valeur maximale et minimale. Donc pour une limite longue égale à 30 (2 / (1 + 30) = 0,0645) et une limite courte égale à 2 (2 / (1 + 2) = 0,6667), la période de la moyenne mobile peut varier entre :
- Si le ER = 0 (niveau d’agitation élevé) : La limite longue est alors égale à 0 x (0,6667 – 0,0645) + 0,0645] puissance 2 = 0,0645 ^ 2 = 0,0042 ce qui correspond à une moyenne mobile de période égale à (2 – 0,0042) / 0,0042 = 480.
- Si le ER = 1 (niveau d’agitation faible) : La limite courte est alors égale à 1 x (0,6667 – 0,0645) + 0,0645] puissance 2 = 0,6667 ^ 2 = 0,4444 ce qui correspond à une moyenne mobile de période de 4.
Par conséquent, si la limite courte est à égale à 2 et limite longue est égale à 30 cela signifie que la période de la moyenne mobile de Kaufman varie entre 4 et 480 selon le niveau d’agitation des cours.
A noter que Kaufman utilise la puissance au carré dans le calcul du facteur d’ajustement pour réduire rapidement la période de la moyenne mobile lorsque le niveau d’agitation est élevé, dans l’exemple ci-dessus, la période est passée de 30 à 480.
Interprétation
Le système de trading utilise la moyenne mobile de Kaufman pour lisser les cours de clôtures sur une période donnée. La tendance est identifiée par la pente de la moyenne mobile. Lorsque la pente de la moyenne mobile change de direction un signal d’achat ou de vente est généré :
- ACHAT (Go Long) : Si la valeur de la moyenne mobile est plus grande que la valeur de la veille
- VENTE (Go Short) : Si la valeur de la moyenne mobile est plus petite que la valeur de la veille
- Pas de changement de signal (Garder le même signal) si la valeur de la moyenne mobile est égale à la valeur de la veille
Au cours du test, la quantité par opération est égale à 1 et aucune commission n’est retenue. Ainsi lorsqu’un signal est généré c’est le cours de clôture qui sera appliqué.
Test du système de tendance
L’évaluation du système de tendance se déroule sur cinq valeurs :
- EUR/USD : Eurodollar Futures
- SPY : SPDR S&P 500 ETF Trust (SPY)
- IEF : iShares 7-10 Year Treasury Bond ETF (IEF)
- XLF : Financial Select Sector SPDR Fund (XLF)
- SMH : VanEck Semiconductor ETF (SMH)
La période de test est de 12 ans, du 01/06/2011 jusqu’au 06/04/2023, il s’agit de la même période déjà utilisée dans le test précèdent. Trois périodes pour le calcul du ratio d’efficacité : 8, 10 et 14, deux périodes pour la limite courte : 10 et 14 et deux périodes pour la limite longue : 20 et 30. En revanche, la valeur de la puissance sera égale à 2.
Les trois tableaux montrent les performances du système de tendance de la moyenne mobile de Kaufman pour la combinaison des trois variables : ratio d’efficacité (8), limite courte (10, 14) et limite longue (20, 30).
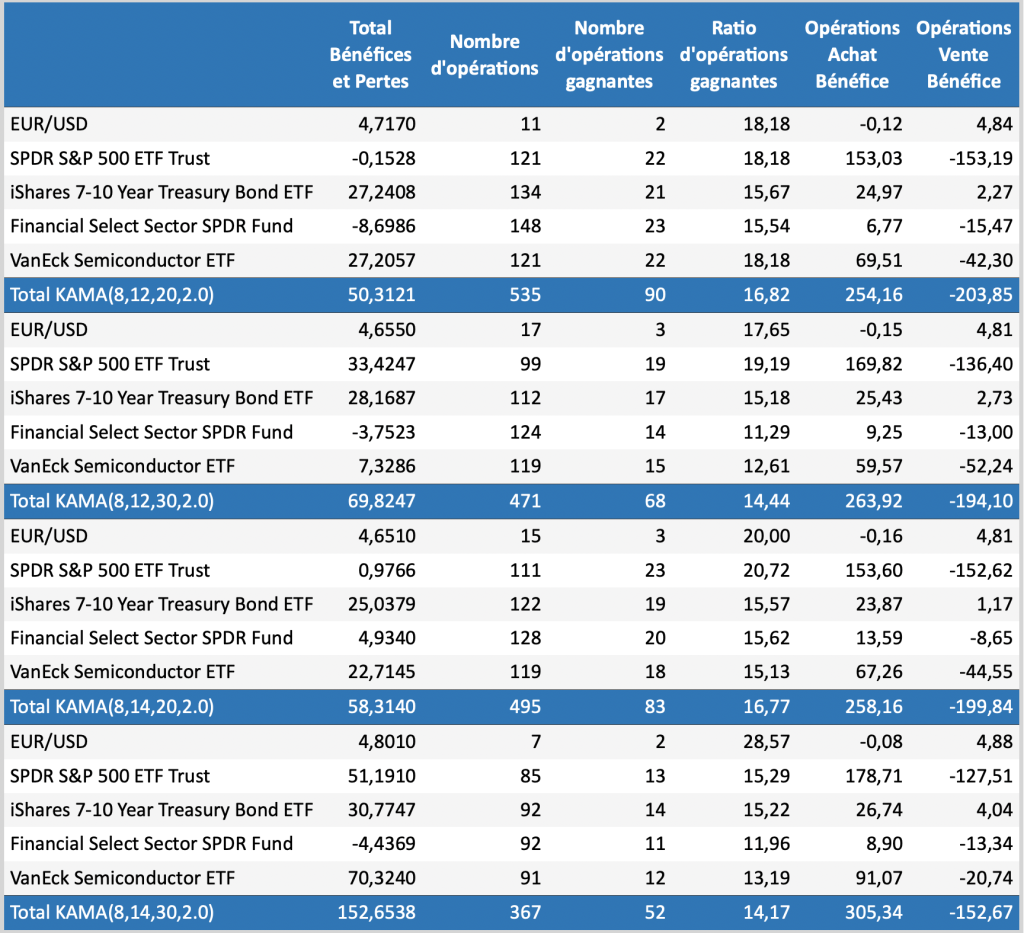
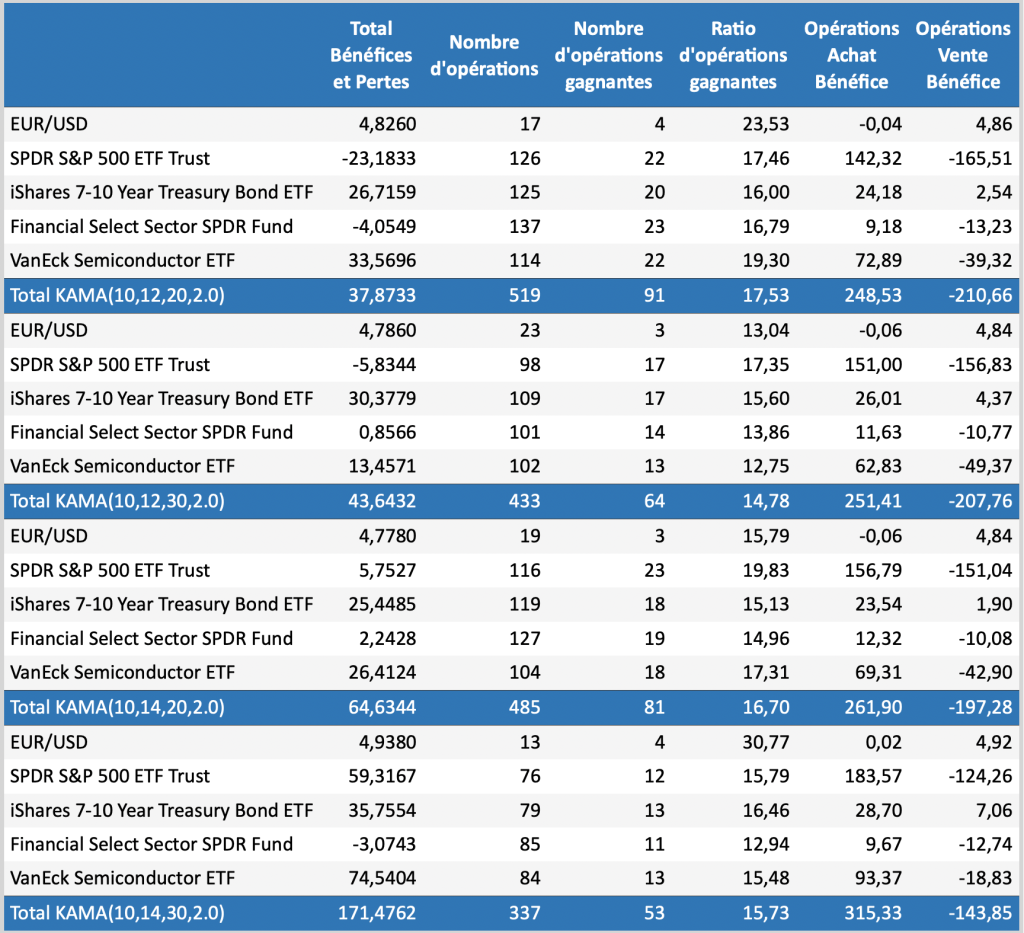
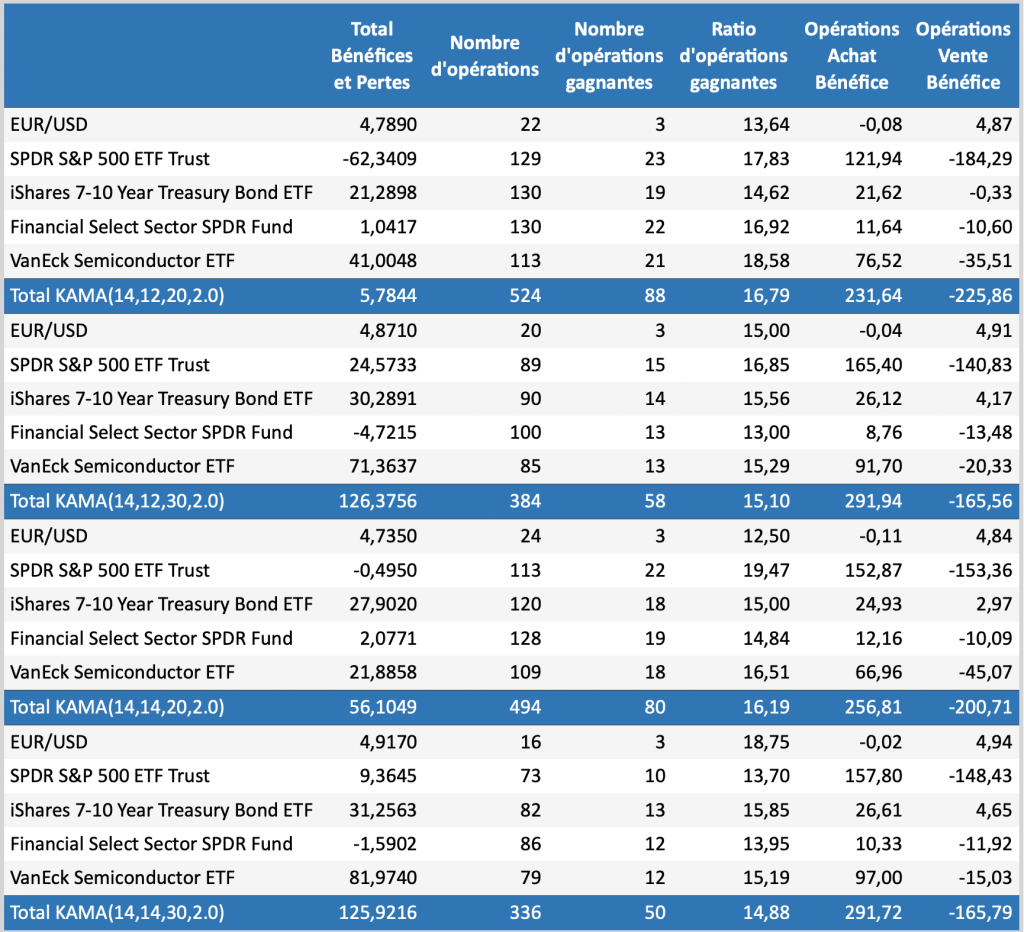
Il est intéressant de constater que le ratio d’opérations gagnantes est dans la majorité des cas en dessous de 30% ce qui signifie que le système n’est pas avantageux. En revanche, les limites de long terme : courte de 14 et longue 30 produisent les meilleures performances dans les trois tableaux avec un nombre réduit de nombre d’opérations ce qui limite le coût des commissions.
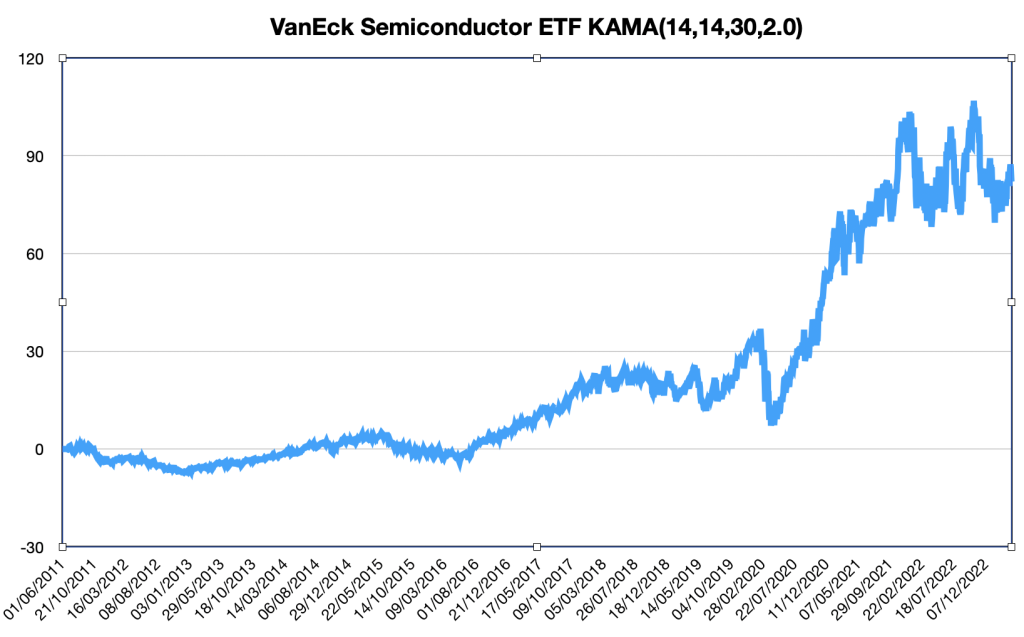
La figure-2 montre l’évolution des bénéfices et des pertes pour la moyenne mobile de Kaufman sur la période du 01/06/2011 au 06/04/2023. Entre 2011 et 2016 le système n’a généré que des faibles bénéfices, puis il fallait attendre 2017 pour que le système commence à performer.
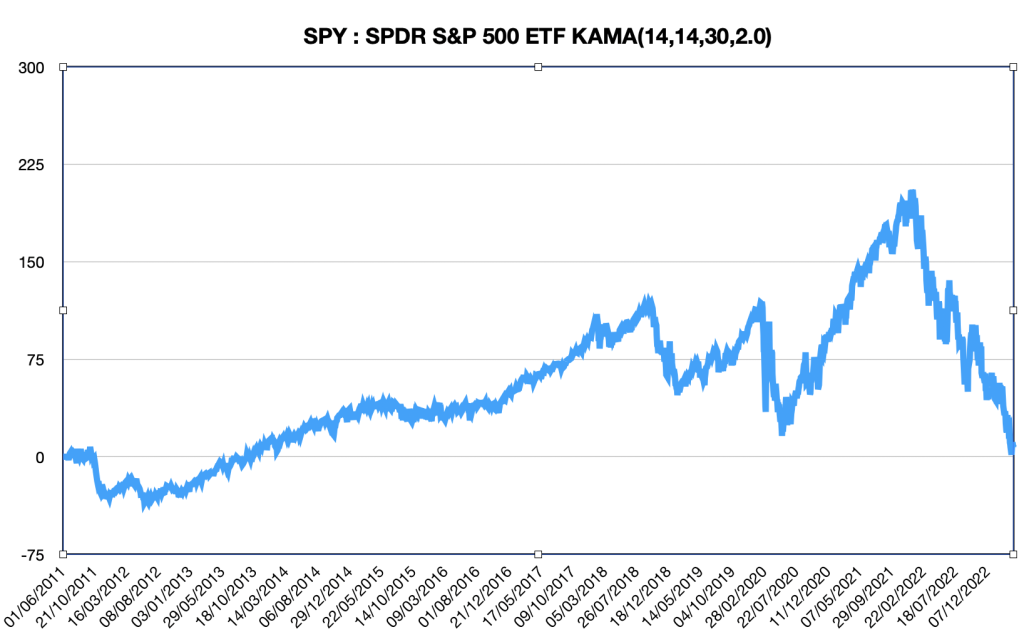
La figure-3 montre l’évolution des bénéfices et des pertes pour la moyenne mobile de Kaufman sur la période du 01/06/2011 au 06/04/2023 sur les cours de SPY. Le début était chaotique, entre 2011 et 2013 le système n’a généré que des pertes, puis à partir de 2014 la performance était correcte jusqu’au 2022 d’où le système a rendu tous les bénéfices accumulés durant 8 ans.
Fichier en format Excel de la moyenne mobile de Kaufman en système de tendance avec des paramètres modifiables (sans macro) : limite longue, limite courte, période de ER, et la puissance, ce qui permet de voir l’évolution du graphique des bénéfices:
Laisser un commentaire